45
Protecting HDDs from (external) train vibrations
(lemmy.dbzer0.com)
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
this post was submitted on 05 Jan 2024
45 points (97.9% liked)
Selfhosted
39677 readers
200 users here now
A place to share alternatives to popular online services that can be self-hosted without giving up privacy or locking you into a service you don't control.
Rules:
-
Be civil: we're here to support and learn from one another. Insults won't be tolerated. Flame wars are frowned upon.
-
No spam posting.
-
Posts have to be centered around self-hosting. There are other communities for discussing hardware or home computing. If it's not obvious why your post topic revolves around selfhosting, please include details to make it clear.
-
Don't duplicate the full text of your blog or github here. Just post the link for folks to click.
-
Submission headline should match the article title (don’t cherry-pick information from the title to fit your agenda).
-
No trolling.
Resources:
- selfh.st Newsletter and index of selfhosted software and apps
- awesome-selfhosted software
- awesome-sysadmin resources
- Self-Hosted Podcast from Jupiter Broadcasting
Any issues on the community? Report it using the report flag.
Questions? DM the mods!
founded 1 year ago
MODERATORS
Hey, great that you chimed in, I agree with the points you're making. As for my remark regarding amplitude, what I wanted to convey was: in the measurement scenario using the PhyBox smartphone app, OP should see an overall smaller signal envelope if the NAS was properly decoupled, compared to the previous plot.
As for your comment regarding the Nyquist theorem, PhyBox maintains a list of devices and their sensors so it would be possible to lookup the available sampling frequency. There are other factors potentially limiting the sample rate (e. g. switching offl microphone access for the app on Android), but it's a good starting point.
https://phyphox.org/sensordb/
However, I think we agree this should be solvable without much theoretical effort.
Wow, I hadn't heard of phyphox before (hadn't even noticed @khorak@lemmy.dbzer0.com mentioned it in the OP). That's very cool and I've installed it now.
I'm wondering, now that you've seen the app, do you have some practical advice on how to measure the difference without having to spend a few hours researching and refreshing on high school physics? It seems that my only option is to run the "Acceleration without g" experiment and work on the csv export.
A probably naive approach would be to filter out values below a certain threshold (a 'low pass filter' of sorts to deal with a noisy sensor) and then try to meaningfully sum the acceleration by time period. But just as I wrote this I realized that I can't simply sum a few values from several rows and call it a day.
The article you linked explained the idea behind the pseudo velocity well, I'm wondering if I can.. "sum the area" (assuming interpolated data) under the various measurement points. Without completely nerding out and investing too much time :D My sensor seems to have a rate of 200Hz, so it should be good for measuring vibrations up to 100Hz.
Edit, it's integrals, right? This is actually exciting, haven't touched math since university. Also here's an example of how the acceleration graph looks like when the phone is on the heating / radiator (more or less worst case):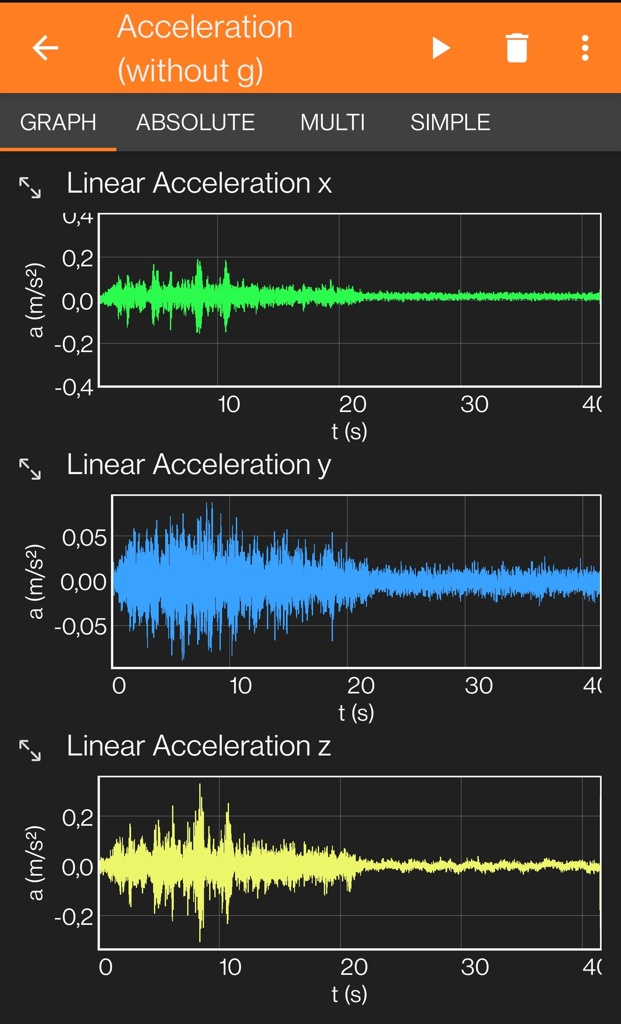
None of the included experiments look to be exactly what you need. For characterizing your isolator, the included Acceleration Spectrum is close, though it records continuously, making it difficult to use to record impact response. For evaluating actual train vibrations, the user-defined Integrated Acceleration might be a start, but it doesn't include the filtering needed to get good information. You could define your own experiments, but that's probably even harder than analyzing the CSV data on your computer. At least on your computer you can change your analysis freely and immediately see results, rather than re-running the experiment every time.
I've been a bit busy so I haven't had the time to figure out what and how much I need to compensate so the sensor data is more useful. One of the sensors seems to be detecting something reminiscent of a sine curve, so this will involve some extra high school math to find a function to cancel it out. Busy dad etc, maybe next week. In the mean time I started putting together the case and ordered the springy subwoofer legs. Here is how a simple plot of the raw acceleration looks like.
It's obvious which one is the before and after. The second one even includes two trains arriving back to back.
Now I need to figure out a few things:
Thanks for the update and graphs. That is an amazing improvement. In the "after" plot, it looks like any acceleration from the train is well below the noise level of your accelerometer. So, within the limits of your measuring equipment, you've effectively eliminated all train vibration. If I were in your place, I would declare success and move on with life! Don't even bother with foam and rubber feet, because this configuration is working great.
But you could analyze further if you really want; there could be some train signal hiding in all that noise. Since there's periodic noise in the Z axis, you could take a reading during a still time (computer off, no trains) and see where your spikes are in the frequency domain. Then you could apply a filter (or filters) to cut out that periodic noise.
But unless you're really into learning about signal analysis, I'd say you could skip it.