758
That's a big burger
(files.catbox.moe)
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
this post was submitted on 28 Aug 2024
758 points (97.6% liked)
Science Memes
11148 readers
2861 users here now
Welcome to c/science_memes @ Mander.xyz!
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.
Rules
- Don't throw mud. Behave like an intellectual and remember the human.
- Keep it rooted (on topic).
- No spam.
- Infographics welcome, get schooled.
This is a science community. We use the Dawkins definition of meme.
Research Committee
Other Mander Communities
Science and Research
Biology and Life Sciences
- !abiogenesis@mander.xyz
- !animal-behavior@mander.xyz
- !anthropology@mander.xyz
- !arachnology@mander.xyz
- !balconygardening@slrpnk.net
- !biodiversity@mander.xyz
- !biology@mander.xyz
- !biophysics@mander.xyz
- !botany@mander.xyz
- !ecology@mander.xyz
- !entomology@mander.xyz
- !fermentation@mander.xyz
- !herpetology@mander.xyz
- !houseplants@mander.xyz
- !medicine@mander.xyz
- !microscopy@mander.xyz
- !mycology@mander.xyz
- !nudibranchs@mander.xyz
- !nutrition@mander.xyz
- !palaeoecology@mander.xyz
- !palaeontology@mander.xyz
- !photosynthesis@mander.xyz
- !plantid@mander.xyz
- !plants@mander.xyz
- !reptiles and amphibians@mander.xyz
Physical Sciences
- !astronomy@mander.xyz
- !chemistry@mander.xyz
- !earthscience@mander.xyz
- !geography@mander.xyz
- !geospatial@mander.xyz
- !nuclear@mander.xyz
- !physics@mander.xyz
- !quantum-computing@mander.xyz
- !spectroscopy@mander.xyz
Humanities and Social Sciences
Practical and Applied Sciences
- !exercise-and sports-science@mander.xyz
- !gardening@mander.xyz
- !self sufficiency@mander.xyz
- !soilscience@slrpnk.net
- !terrariums@mander.xyz
- !timelapse@mander.xyz
Memes
Miscellaneous
founded 2 years ago
MODERATORS
how can I calculate the distance at which the sun filled my entire field of view?
Theta = 1/2 human fov
r = radius of sun
so simple (and not at all). Thanks.
https://lemmy.ca/comment/11296009
Thanks, you saved the day.
If you're so good at maths, can you tell me how a cord devide the radius? Or something to that extent. I know the chord's lenght, and the minor segment's height. Now to modell this I probly need a cylinder and cut the major segment off, but to get the right size I need the r. Don't I? Am I going insane?
edit: lmao google IS my friend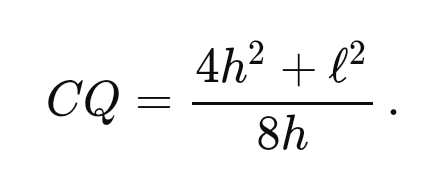
d = r/sinΘ
Human FoV is about 210° with both eyes. Thus Θ is 105°.
The radius of the sun is 695,508 km.
Thus, d is 695,508/sin(105) → 720,043 km
720,043 - 695,508 = 24535 km away from the surface of the sun.
However, because the FoV is greater than 180°, this is actually below the surface of the sun, and any distance below the surface is enough to fill your vision.
To completely fill your field of view with the Sun, you'll need to take a Parker Bath and dip into the sun.
I think 210° is when you moved your eyes to the limit at both sides. So let's say it's FOV when your eyes look straight forward and don't move.
The 210 is straight ahead horizontal FOV, i just didn't realize it was greater than 180°, which means it can technicaly never completely fill your peripheral vision. Your binocular vision with both eyes is around 115°. Vertical fov is only 135° though.